Proyección ortogonal de un punto sobre un vector:

\[\vec{proj_{a}(x)} = \lambda \vec{a} \\\] \[\vec{r} = \vec{x} - \vec{proj_{a}(x)} \\\]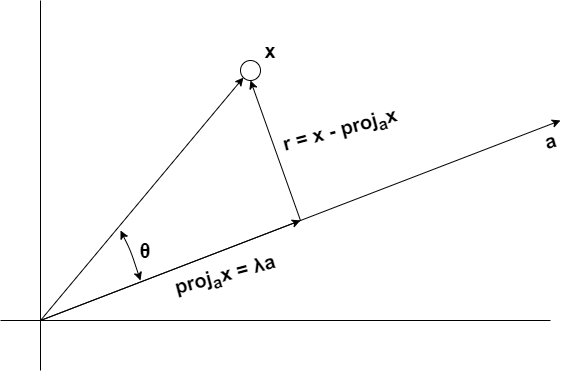

Dado que \(\vec{a}\) y \(\vec{r}\) forman 90 grados, el producto escalar de ambos será 0:

\[<\vec{a}, \vec{r}> = \vec{a}^{t}\vec{r} = \vec{a}^{t}(\vec{x} - \vec{proj_{a}(x)}) = \vec{a}^{t}(\vec{x} - \lambda \vec{a}) = 0 => \\\] \[\vec{a}^{t}\vec{x} - \vec{a}^{t}\lambda \vec{a} = 0 => \vec{a}^{t}\vec{x} = \vec{a}^{t}\lambda \vec{a} => \\\] \[\vec{a}^{t}\vec{x} = \lambda\vec{a}^{t}\vec{a} => \lambda = \frac{\vec{a}^{t}\vec{x}}{\vec{a}^{t}\vec{a}} \\\]

Dado que ya conocemos el valor del escalar \(\lambda\), sustituimos en la ecuación de la proyección:

\[\vec{proj_{a}(x)} = \lambda \vec{a} = \frac{\vec{a}^{t}\vec{x}}{\vec{a}^{t}\vec{a}}\vec{a}\]

Bajo el supuesto de que el vector \(\vec{a}\) sea unitario por restricción impuesta(se verá más adelante), se tiene que:

\[\vec{a}^{t}\vec{a} = \left[\frac{a_{1}}{||a||}, ..., \frac{a_{p}}{||a||}\right] \left[\begin{array}{@{}c@{}} \frac{a_{1}}{||a||} \\ \vdots \\ \frac{a_{p}}{||a||} \end{array} \right] = \\\] \[(\frac{a_{1}}{||a||})^{2} + ... + (\frac{a_{p}}{||a||})^{2} = \\\] \[\frac{a_{1}^{2}}{(\sqrt{a_{1}^{2} + ... + a_{p}^{2}})^{2}} + ... + \frac{a_{p}^{2}}{(\sqrt{a_{1}^{2} + ... + a_{p}^{2}})^{2}} =\\\] \[\frac{a_{1}^{2} + ... + a_{p}^{2}}{a_{1}^{2} + ... + a_{p}^{2}} = 1 \\\]

Por tanto, se puede rescribir el vector proyección \(\vec{proj_{a}(x)}\) como sigue:

\[\vec{proj_{a}(x)} = \frac{\vec{a}^{t}\vec{x}}{1}\vec{a} = \vec{a}^{t}\vec{x}\vec{a} = \lambda\vec{a} => \lambda = \vec{a}^{t}\vec{x}\\\]

Su módulo quedaría:

\[||\vec{proj_{a}(x)}|| = \left. ||\vec{a}^{t}\vec{x}\vec{a}|| \right\rvert_{\vec{a}^{t}\vec{x} = \lambda} = ||\lambda\vec{a}|| = \lambda||\vec{a}|| = (\vec{a}^{t}\vec{x})||\vec{a}|| \\\] \[\lambda = \vec{a}^{t}\vec{x} = \sum_{i=1}^{p} a_{1i}x_{i1} \\\]

La proyección del punto sobre el vector, \(\left \| \vec{proj_{a}(x)} \right \|\) vendrá a representar la contribución de dicho punto sobre la varianza de la componente principal.

El residuo cometido, \(\left \| \vec{r} \right \|\) vendrá a representar la contribución de dicho punto sobre la varianza perdida al usar la componente principal.