Cada peso sufre una pequeña perturbación, \(\Delta W_{ij}\), como sigue:

\[W_{ij} := W_{ij} + \Delta W_{ij} \\\]

Dicha perturbación no es aleatoria, está escogida en la dirección inversa a la dirección de máximo ascenso del error cometido, esto es, la dirección inversa de la dirección dada por el gradiente de la función que expresa el error cometido por la red neuronal, y que depende del vector de pesos de la red.

\[- \nabla_{\vec w} \mathcal{C} = - \left[\begin{array}{@{}c@{}} \frac{\partial C}{\partial w_{1}} \\ \vdots \\ \frac{\partial C}{\partial w_{n}} \end{array} \right] \\\] \[-\frac{\partial C}{\partial W_{ij}} \\\]

Cada actualización de pesos se interpreta como un paso adelante en la dirección de máximo descenso de la función error de la red neuronal:

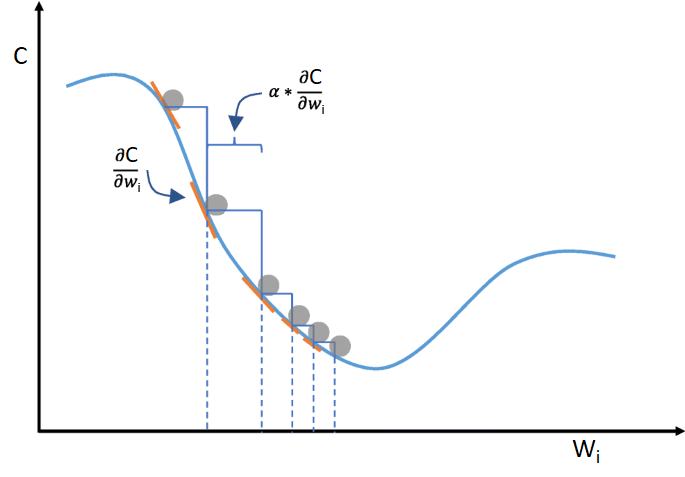
El tamaño de dicho paso, \(\alpha\), un valor entre 0 y 1 que marca la tasa de aprendizaje que es empleada durante el entrenamiento, es un hiperparámetro a encontrar.

Aunque su magnitud podría variar en diferentes etapas del aprendizaje:

• tasas mayores implica saltos más grandes en el espacio de búsqueda, lo cual nos permite buscar mínimos deseados en otras zonas más alejadas del espacio.
• tasas menores implica saltos más pequeños en el espacio de búsqueda, lo cual nos permite profundizar la búsqueda en una zona muy concreta del espacio en la cual hayamos puesto atención.

La perturbación final que sufre el peso en la actualización quedaría como sigue:

\[\Delta W_{ij} = \alpha(-\frac{\partial C}{\partial W_{ij}}) = -\alpha\frac{\partial C}{\partial W_{ij}} \\\] \[W_{ij} := W_{ij} + (-\alpha\frac{\partial C}{\partial W_{ij}}) = W_{ij} - \alpha\frac{\partial C}{\partial W_{ij}}\\\]

La derivada parcial puede ser descompuesta, teniendo presente que una perturbación no afecta directamente en el coste final, sino que lo hace a la entrada de la neurona, y esta a su vez propaga la perturbación al coste final:

\[\frac{\partial C}{\partial w_{1i}^{n-1}} = \frac{\partial C}{\partial a_{1}^{n}}\frac{\partial a_{1}^{n}}{\partial w_{1i}^{n-1}} \\\]

La resolución de la derivada parcial, como parte del vector gradiente, quedaría como sigue:

\[\frac{\partial C}{\partial w_{1i}^{n-1}} = \left. \frac{\partial C}{\partial a_{1}^{n}}\frac{\partial a_{1}^{n}}{\partial w_{1i}^{n-1}} \right\rvert_{\frac{\partial C}{\partial a_{1}^{n}} = \delta_{1}^{n}}= \\\] \[\left. \delta_{1}^{n}\frac{\partial a_{1}^{n}}{\partial w_{1i}^{n-1}} \right\rvert_{a_{1}^{n} = b_{1}^{n-1} + \sum_{i=1}^{r_{n-1}} w_{1i}^{n-1} o_{i}^{n-1} } = \\\] \[\delta_{1}^{n}\frac{ \partial (b_{1}^{n-1} + \sum_{i=1}^{r_{n-1}} w_{1i}^{n-1} o_{i}^{n-1}) }{\partial w_{1i}^{n-1}} = \\\] \[\delta_{1}^{n} \left( \frac{\partial b_{1}^{n-1}}{\partial w_{1i}^{n-1}} + \frac{\partial (\sum_{i=1}^{r_{n-1}} w_{1i}^{n-1} o_{i}^{n-1})}{\partial w_{1i}^{n-1}} \right) = \\\] \[\delta_{1}^{n} \left( 0 + \frac{\partial (\sum_{i=1}^{r_{n-1}} w_{1i}^{n-1} o_{i}^{n-1})}{\partial w_{1i}^{n-1}} \right) = \\\] \[\delta_{1}^{n} \frac{\partial (\sum_{i=1}^{r_{n-1}} w_{1i}^{n-1} o_{i}^{n-1})}{\partial w_{1i}^{n-1}} = \\\] \[\delta_{1}^{n} \left(\frac{\partial w_{1i}^{n-1} o_{i}^{n-1}}{\partial w_{1i}^{n-1}} + \frac{\partial (\sum_{\substack{k=1 \\ k\neq i}}^{r_{n-1}} w_{1k}^{n-1} o_{k}^{n-1})}{\partial w_{1i}^{n-1}} \right) = \\\] \[\delta_{1}^{n} \left(\frac{\partial w_{1i}^{n-1} o_{i}^{n-1}}{\partial w_{1i}^{n-1}} + 0 \right) = \\\] \[\delta_{1}^{n} \left(\frac{\partial w_{1i}^{n-1} o_{i}^{n-1}}{\partial w_{1i}^{n-1}} \right) = \\\] \[\delta_{1}^{n}o_{i}^{n-1}\frac{\partial w_{1i}^{n-1}}{\partial w_{1i}^{n-1}} = \\\] \[\delta_{1}^{n}o_{i}^{n-1}1 = \\\] \[\delta_{1}^{n}o_{i}^{n-1} = \\\] \[\left. \delta_{1}^{n}o_{i}^{n-1} \right\rvert_{j=1} = \\\] \[\delta_{j}^{n}o_{i}^{n-1} = \\\] \[\left. \delta_{j}^{n}o_{i}^{n-1} \right\rvert_{\substack{\delta_{j}^{n} = (o_{j}^{n}-y_{j}^{n}) {g}'(a_{j}^{n})}} = \\\] \[\delta_{j}^{n}o_{i}^{n-1} = (o_{j}^{n}-y_{j}^{n}){g}'(a_{j}^{n})o_{i}^{n-1} \\\]

La actualización final del peso, sustituyendo la derivada parcial \(\frac{\partial C}{\partial w_{1i}^{n-1}}\) por su resolución, quedaría como sigue:

\[W_{ij} := W_{ij} - \alpha(o_{j}^{n}-y_{j}^{n}){g}'(a_{j}^{n})o_{i}^{n-1} \\\]